Multivariate Normal Distribution

 Multivariate Normal Distribution

Easy:

Imagine you have a box of crayons that can make any color you want just by mixing them together. Now, let’s say you have three different colors: red, blue, and green. If you mix these colors in equal amounts, you get a beautiful shade of purple.

But what if you don’t use equal amounts? Maybe you add more red than blue and green, or maybe you mix them in different ways each time. The result will always be some shade of purple, but it might look slightly different every time because of how much of each color you used.

Now, imagine if instead of just three colors, you had many, many crayons, and you could mix them all together in endless combinations. That’s kind of like what a multivariate normal distribution is, but instead of colors, we’re talking about numbers.

In a multivariate normal distribution, you have lots of different numbers (or variables) that can change and combine in many ways. Just like how you can create many shades of purple by mixing your crayons, you can create many different outcomes by combining these numbers in different ways.

The “normal” part means that most of the time, when you mix these numbers together, you’ll end up with something that looks pretty average or typical. It’s like saying that if you keep mixing your crayons, most of the time, you’ll probably get a nice, bright purple.

So, a multivariate normal distribution is just a fancy way of saying that when you have lots of numbers that can mix and match in many ways, most of the time, the results will be pretty average and predictable.

Crayons

Moderate:

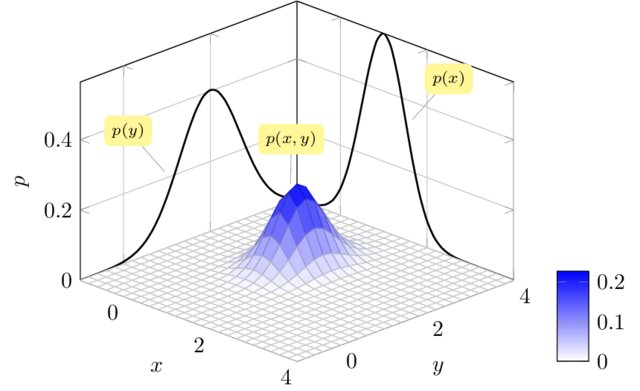
Multivariate Normal Distribution is a statistical concept that describes the probability distribution of multiple variables at once. Imagine you’re dealing with a set of data points where each point has several characteristics or features. For example, consider a group of people, each described not only by their height but also by their weight, age, and shoe size. In this scenario, each person’s height, weight, age, and shoe size are variables.

A univariate normal distribution deals with one variable at a time, like the heights of people. A bivariate normal distribution considers two variables, such as both height and weight. However, a multivariate normal distribution goes further, encompassing three or more variables simultaneously.

Key Characteristics:

  1. Mean Vector: This is the center point of the distribution, representing the average values of all variables. For our example, it would include the mean height, mean weight, etc.
  2. Covariance Matrix: This matrix shows how each variable interacts with every other variable. High positive values indicate a strong direct relationship between variables (e.g., taller people tend to weigh more), while high negative values suggest an inverse relationship (e.g., older people tend to be shorter). Diagonal elements represent the variance of each variable, indicating how much each variable differs from its mean on average.
  3. Independence: In a perfect multivariate normal distribution, variables are independent, meaning the value of one does not affect the others. In reality, variables often have some degree of dependence.
  4. Normality: Each variable follows a univariate normal distribution when considered independently. This means the distribution of each variable, if plotted, would form a bell curve.
  5. Bell Curve for Each Variable: Even though we’re looking at multiple variables, each individual variable (if isolated) would still follow a normal distribution, appearing as a bell curve when graphed.

Practical Use:

Multivariate Normal Distribution is crucial in statistics for understanding complex datasets where relationships among various factors need to be analyzed. It’s used in fields ranging from finance (to model returns on multiple assets) to genetics (to understand how different traits are inherited).

Example:

Imagine you’re trying to predict a student’s final grade based on their scores in three subjects: Math, Science, and English. If these scores follow a multivariate normal distribution, you can use statistical methods to understand how these subjects relate to each other and to the final grade. This could help identify if students who perform well in Math also tend to do well in Science and English, or if there’s no correlation between these subjects.

In summary, Multivariate Normal Distribution is a powerful tool for analyzing and predicting relationships among multiple variables, providing insights into complex datasets.

Hard:

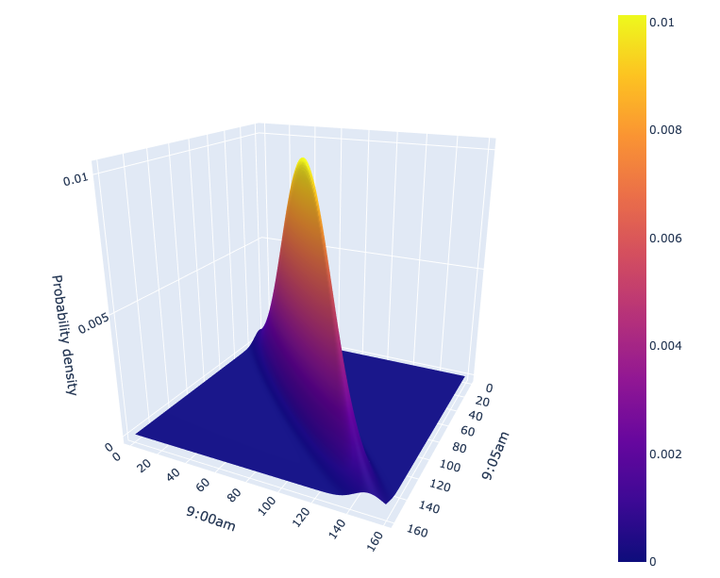
The multivariate normal distribution is a generalization of the univariate (one-dimensional) normal distribution to multiple dimensions. It describes a probability distribution over vectors in a d-dimensional space, where d is a positive integer.

A random vector X = (X1, X2, …, Xd) follows a multivariate normal distribution if its density function can be written as:

f(x) = (1 / (sqrt((2π)^d * |Σ|))) \* exp(-0.5 \* ((x — μ)’ \* Σ^-1 \* (x — μ)))

where:

* x is a column vector representing a particular point in the d-dimensional space;

* μ is a column vector of means for each dimension;

* Σ is the covariance matrix, which encodes information about the variances and correlations among the different dimensions;

* |Σ| denotes the determinant of the covariance matrix;

* ‘ denotes the transpose operator;

* exp() is the exponential function.

The multivariate normal distribution is completely specified by its mean vector μ and covariance matrix Σ. Intuitively, the mean vector gives the center of mass of the distribution, while the covariance matrix captures the shape and orientation of the ellipsoidal contours of equal probability. In particular, the eigenvectors of the covariance matrix determine the directions of the principal axes of the ellipse, while the corresponding eigenvalues give the lengths of those axes.

One important property of the multivariate normal distribution is that linear transformations preserve normality. That is, if X follows a multivariate normal distribution and A is a constant matrix, then the transformed random vector Y = AX also follows a multivariate normal distribution, with mean vector μ\_Y = Aμ and covariance matrix Σ\_Y = AΣA’. This property makes the multivariate normal distribution particularly useful in many areas of statistics, including hypothesis testing, regression analysis, and machine learning.

A few books on deep learning that I am reading:

Book 1

Book 2

Book 3

Comments

Post a Comment

Popular posts from this blog

Mid Level Depth Aware Semantic Segmentation

Image
Mid Level Depth Aware Semantic Segmentation Easy: Imagine you’re playing a game where you have to draw a picture of a scene, but you can only use one color for everything. Now, imagine you’re playing this game in a room with a lot of different things in it, like toys, a bed, and a toy box. You want to make sure that your drawing looks realistic, so you need to figure out how to use your one color to make everything look like it’s in the right place and at the right distance from each other. Mid Level Depth Aware Semantic Segmentation is like that game, but for computers. Computers use something called “machine learning” to help them understand and draw pictures of real-world scenes. When they do this, they need to know where everything is and how far away it is from the camera. This is what we call “depth” in computer vision. But there’s a twist! Just like in your game, the computer can only use one color for everything. So, it needs to figure out what each thing in the scene is (like ...
Read more

Blind Super Resolution Generative Adversarial Network(BSRGAN)

Image
Blind Super Resolution Generative Adversarial Network(BSRGAN) Easy: Imagine you have a super special toy camera that can take pictures of things that are too far away or too blurry for your regular camera to capture clearly. But sometimes, when you try to take a picture with this special camera, it doesn’t work perfectly because the image is still not clear enough. Now, let’s say there’s a magical friend who loves puzzles and games. This friend has a magic wand that can help make those unclear images clearer. The magic wand works in a very special way: it looks at the blurry image from the special camera and tries to guess what the image should look like if everything was perfect. It then draws over the blurry image with its magic, making it clearer and more detailed. But here’s the twist — our magical friend doesn’t just randomly draw on the image. They play a game where they try to trick another magical friend into thinking the new, clearer image is real and not something they made u...
Read more

Explain Denoising Score Process Matching(DSM)

Image
Explain Denoising Score Process Matching(DSM) Easy: Imagine you have a big box of mixed-up toys. Some toys are broken, some are missing pieces, and others are just plain dirty. Your job is to sort these toys so that each toy is clean, fixed, and ready to play with. This process is similar to what we call Denoising Score Process Matching (DSM). In DSM, computers help us do something very special: they look at a bunch of pictures or sounds and try to find the best match even if it’s been changed or messed up in some way. It’s like finding the perfect puzzle piece that fits into your mixed-up picture. Here’s how it works: Collecting Information: First, the computer collects lots of examples of what it should be looking for. For example, if we’re trying to fix a noisy sound, the computer might listen to many clear, high-quality versions of the same sound. Learning Patterns: Next, the computer learns from these examples. It figures out what makes them good and tries to apply those rules t...
Read more